Conducting a Two Proportion Z-Test using SPSS is a statistical analysis technique used to compare the proportions of two independent groups. This test is often used in research studies to determine if there is a significant difference between the proportions of two variables. It enables researchers to make informed decisions and draw conclusions based on the data collected. In this guide, we will discuss the steps involved in conducting a Two Proportion Z-Test using SPSS, including the preparation of data, performing the test, and interpreting the results. With the help of this guide, you will be able to confidently conduct this statistical analysis and make evidence-based decisions in your research.

A Two Proportion Z-Test is a statistical analysis method used to determine if there is a significant difference between two proportions in a population. To perform this test in SPSS, one must first input the data for the two groups being compared. Then, the appropriate test must be selected from the Analyze menu and the required variables must be chosen. The results of the test, including the p-value and confidence interval, will be displayed in the output window. This test can be used to make informed decisions and draw conclusions about the differences between two proportions.

Perform a Two Proportion Z-Test in SPSS

A two proportion z-test is used to test for a difference between two population proportions.

The easiest way to perform a two proportion z-test in SPSS is by using Analyze> Descriptive Statistics > Crosstabs.

The following example shows how to do so in practice.

Example: Two Proportion Z-Test in SPSS

Suppose a teacher believes that the proportion of her students in both of her classes who prefer a specific teaching method is equal.

To test this, she surveys the 30 students in each class and receives the following results:

Class A Size: 30
Count in Class A who prefer method: 23
Class B Size: 30
Count in Class B who prefer method: 18

Here is how to enter this data into SPSS:

Before we perform the two proportion z-test to determine if the two proportions are equal, we must first weight the cases.

To do so, click the Data tab, then click Weight Cases.

In the new window that appears, drag the Count variable into the Frequency variable panel:

Then click OK.

Then click the Analyze tab, then click Descriptive Statistics, then click Crosstabs:

In the new window that appears, drag the Class variable to the Rows panel and drag the Preference variable to the Columns panel:

Then click the Statistics button.

In the new window that appears, check the box next to Chi-square:

Then click Continue. Then click OK.

The following output will be generated:

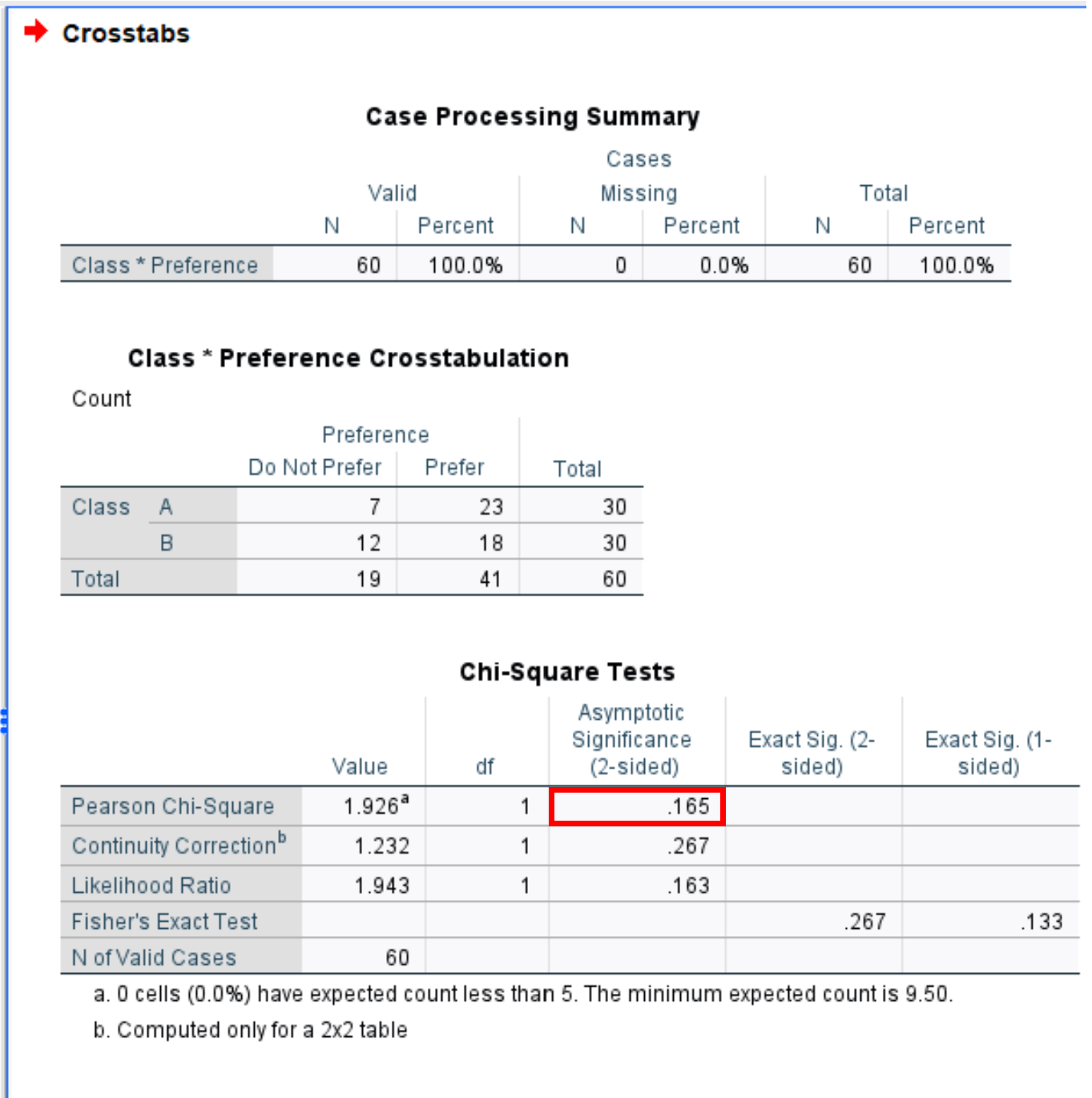
The two-tailed p-value for the two proportion z-test is shown in the final table of the output in the Pearson Chi-Square row.

In this particular example the p-value for the two proportion z-test is .165.

The two proportion z-test uses the following hypotheses:

H₀: The two population proportions are equal.
H_A: The two population proportions are not equal.

Since our p-value (.165) is less than .05, we fail to the null hypothesis.

Thus, we do not have sufficient evidence to say that the proportion of students in each class who prefer the specific teaching method is different.

Bonus: You can also use the arabpsychology .

Additional Resources

The following tutorials explain how to perform other common tasks in SPSS:

@media(max-width:1200px){}.novashare-inline:not(.novashare-columns) .novashare-buttons-wrapper{justify-content:center;}body .novashare-inline:not(.novashare-columns) a.novashare-button, body .novashare-inline .novashare-total-share-count{margin:0px 5px 10px 5px;}body .novashare-buttons.novashare-inline .novashare-button-icon{width:100%;}